資金計画で使える『6つの係数』の存在だけは知っておいて欲しい！すっごく便利なんですよ！

資金計画（ライフプランニング）する時に、すっごく便利なのが『6つの係数』です。

これは複利運用をした場合の計算を簡単にしてくれるものなのです。

100万円を利率3％で5年の複利運用をした場合に、100万円が5年後にいくらになるかを計算すると下記のようになります。

1. 1,000,000×1.03=1,030,000
2. 1,030,000×1.03=1,060,900
3. 1,060,900×1.03=1,092,727
4. 1,092,727×1.03=1,125,509
5. 1,125,509×1.03=1,159,274

5回も計算して、やっと5年後の金額が出せましたよね。これを1回の計算でやってくれるのが下の表です。

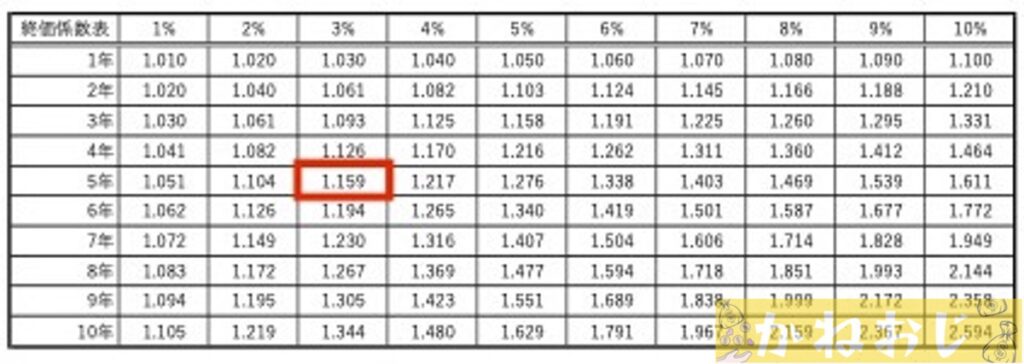
上の表は『終価係数』という係数の表なのですが、100万円に赤枠で囲った数字をかけてみると、1,159,000と先ほどの答えとほとんど同じ金額が出ましたね。

これが今回お伝えしたい『6つの係数』の便利なところです。

この係数がいつ、どんな時に使えるのかをお伝えしますので、「”6つ係数”と呼ばれるものがあるんだな」ぐらいに覚えておいて下さい。

そしていざライフプランニングしよう！と考えた時には、ぜひとも活用してみて下さい。

ライフプランニングで使える『6つの係数』

終価係数

『終価係数』は、手元にあるお金を複利運用した場合に、将来いくらになるか？を求める時に使えます。

今100万円持っているんだけれど、10年後に150万円まで増やしたい場合は年利何％で運用すればいいんだろう？ってことも簡単にわかっちゃいますよ。（ちなみに答えは4.15％です）

現価係数

『現価係数』は、将来必要な金額から逆算して、今いくら必要なのか？を求める時に使えます。

「子供の大学入学資金として400万円必要だから、それまでの20年間で3％の複利運用をすると想定したら、今必要な金額はいくらだろう？」って疑問にすぐ答えが出せます。（ちなみに答えは221万6千円です）

年金終価係数

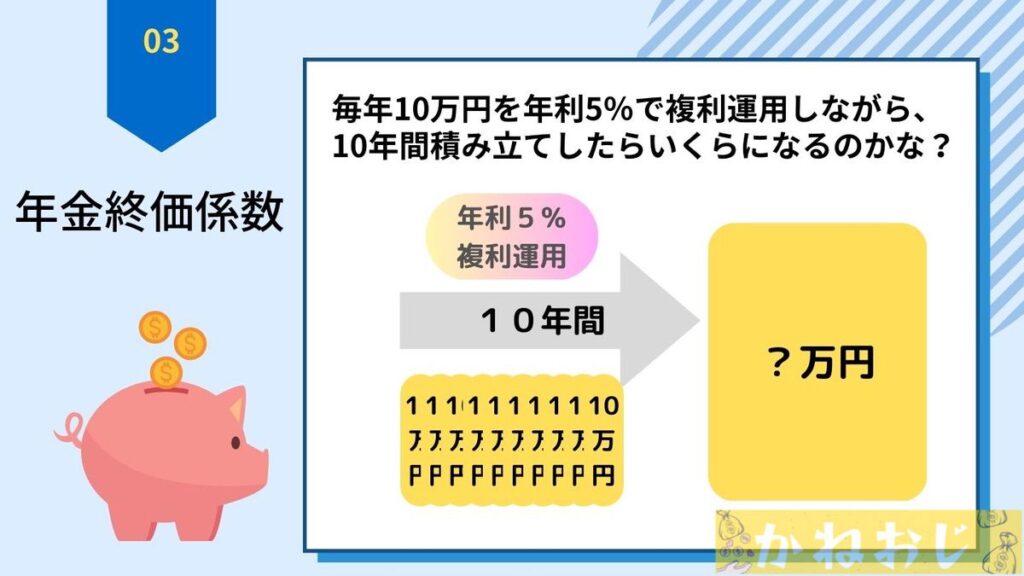
『年金終価係数』は、毎年同じ金額を積み立てしながら、そのお金を複利運用した場合に、将来いくらになるのか？を求める時に使えます。

単純に10万円を10年間積み立てしただけなら、10万円×10年=100万円という金額がわかりますが、積み立てしつつ複利運用した場合には計算式が複雑になりますので、『年金終価係数』が役に立ちますよ。

ちなみに10万円を10年間、年利5％の複利運用をしながら積み立て場合には、10万円×12.578=125万7800円とすぐにわかります。

この10万円に掛けた12.578という乗数は、『年金終価係数』の表を見ることでわかるのですが、最後に紹介している計算サイトに「年利率」と「積立年数」を入力するだけで簡単に出てきます。

減債基金係数

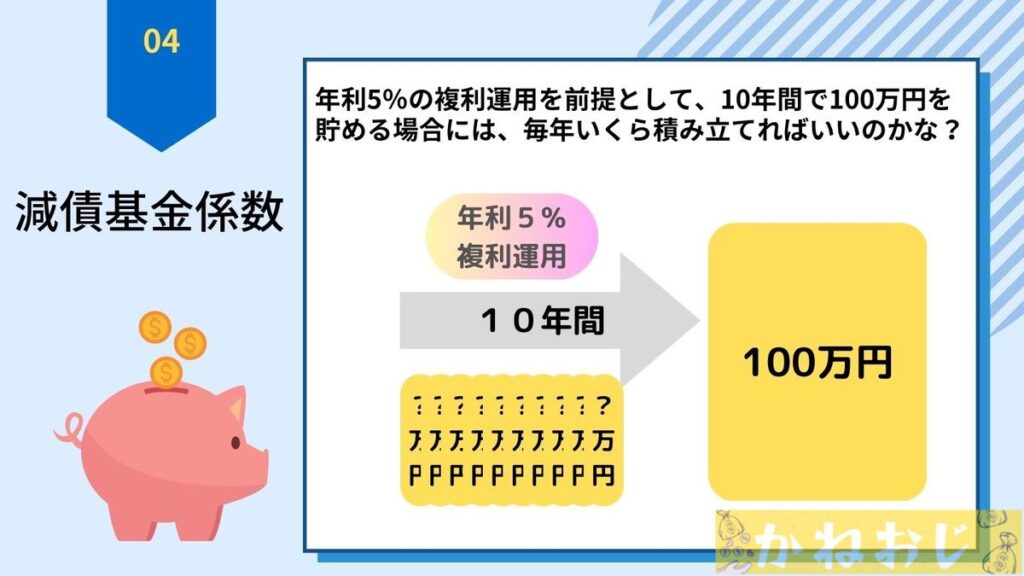
『減債基金係数』は、将来必要な額から逆算して、毎年いくらを積み立てればいいのか？を計算する時に使えます。

こちらは先ほどの『年金終価係数』の逆で、単純に100万円を10年間で貯めるなら、毎年10万円を積み立てればいいのですが、積み立てしつつ複利運用した場合には、10万円よりも少ない金額で100万円が貯まりますからね。

ちなみに年利5％の複利運用をしつつ、10年間で100万円を貯めるには、100万円×0.080=8万円という金額になります。

これも下記の計算サイトで『減債基金係数』の欄を見るとすぐにわかりますよ。

年金現価係数

『年金現価係数』は、一定の金額を毎年受け取りたい場合に、今いくら必要なのか？を調べたい時に使えます。

60歳から70歳までの10年間に、年利5％の複利運用をしながら、毎年10万円を受け取りたいと考えた時、60歳までにいくらを貯めておけばいいのかがわかります。

老後の年金計算をする時に最適ですね。（ちなみに60歳までに77万2,200円の元本があれば、10年間10万円ずつ取り崩すことができます）

資本回収係数

『資本回収係数』は、手元にあるお金を基に、毎年いくらずつ受け取れるのか？を求める時に使えます。

例えば60歳までに500万円を貯めたとしたら、それを年利5％で運用しつつ、10年間で取り崩そうと考えた場合には、500万円×0.130=65万円とわかります。

ただ単純に500万円の貯金を10年で取り崩そうと考えたら、毎年50万円ずつしか受け取れないんですけどね。複利運用することで、毎年15万円も多い金額を受け取れるとわかります。

まとめ

今回お伝えした『6つの係数』の便利さをおわかりいただけましたでしょうか？

子供の教育資金、住宅購入費用、老後の資金などなど、何年か後のことを計算したいって時に、『6つの係数』が計算をとっても簡単にしてくれます。

『6つの係数』の表は、インターネットを検索することで簡単に表を見つけることができます。

しかし文中でもお伝えした通り、表を使わずとも下記のサイト（電卓や電子辞書で有名な『CASIO』さんが運営している）で、一度に6つの係数の結果を出すことができます。

ぜひ一度試しに使ってみて下さい。

参考

資産運用の6つの係数

高精度計算サイト

お金の計算をしていく上で、複利の計算は欠かせませんからね。

少しずつ複利の計算にもふれながら、一緒にお金の勉強をしていきましょう！

最後までお読みいただきまして、誠にありがとうございました。